We have already studied the surface areas of cube, cuboid and cylinder. Now we will explore surface areas and volumes of cones, spheres, and hemispheres.
11.1 Surface Area of a Right Circular Cone
Understanding Cone Formation
When you take a right-angled triangle ABC (right angled at B) and paste a string along one perpendicular side AB, then rotate the triangle about this string, the triangle forms a cone – specifically a right circular cone.
A (vertex)
/|
/ |
/ | h (height)
/ |
/ |
/_____|
C B
r (radius)In a right circular cone:
- Point A is the vertex
- AB is the height (h)
- BC is the radius (r)
- AC is the slant height (l)
- B is the centre of the circular base
The measurements are connected by: l² = r² + h²
Deriving the Curved Surface Area
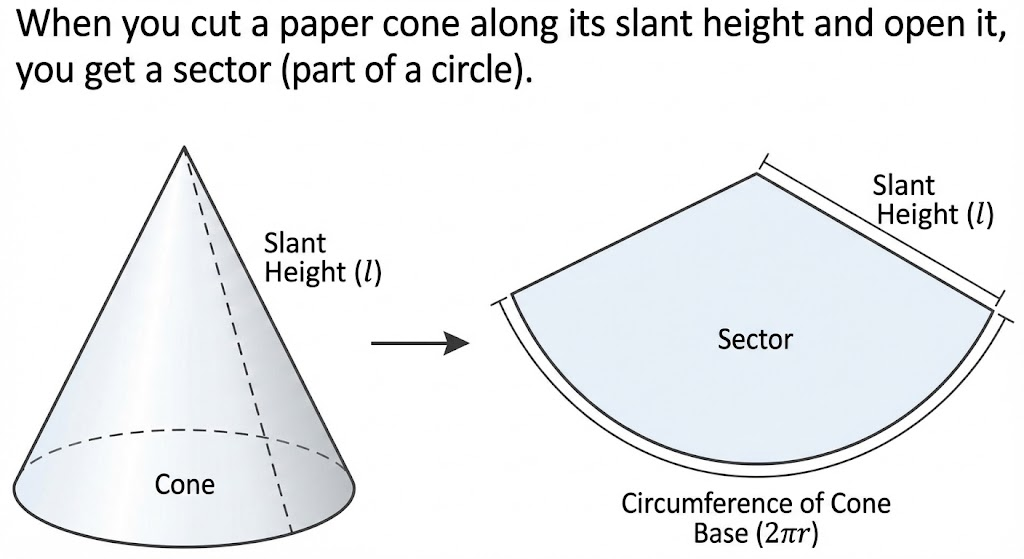
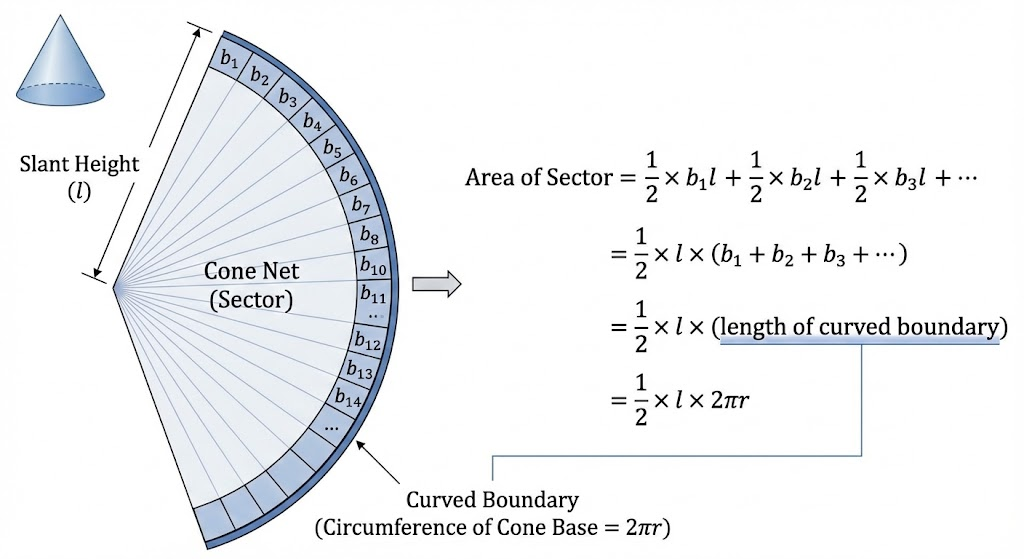
Curved Surface Area of a Cone = πrl
where r is base radius and l is slant height.
Since l² = r² + h², we have l = √(r² + h²)
For a closed cone, we add the base area πr²:
Total Surface Area of a Cone = πrl + πr² = πr(l + r)
Example 1
Find the curved surface area of a right circular cone whose slant height is 10 cm and base radius is 7 cm.
Solution:
Curved surface area = πrl
= (22/7) × 7 × 10 cm²
= 220 cm²
Example 2
The height of a cone is 16 cm and its base radius is 12 cm. Find the curved surface area and the total surface area of the cone. (Use π = 3.14)
Solution:
Here, h = 16 cm and r = 12 cm
From l² = h² + r²:
l = √(16² + 12²) cm
l = √(256 + 144) cm
l = √400 cm
l = 20 cm
Curved surface area = πrl
= 3.14 × 12 × 20 cm²
= 753.6 cm²
Total surface area = πrl + πr²
= 753.6 + (3.14 × 12 × 12) cm²
= 753.6 + 452.16 cm²
= 1205.76 cm²
Example 3
A corn cob, shaped like a cone, has radius 2.1 cm and length 20 cm. If each 1 cm² of surface carries 4 grains, find how many grains are on the entire cob.
Solution:
We need to find slant height first:
l = √(r² + h²)
l = √((2.1)² + 20²) cm
l = √404.41 cm
l = 20.11 cm (approx.)
Curved surface area = πrl
= (22/7) × 2.1 × 20.11 cm²
= 132.73 cm² (approx.)
Number of grains = 132.73 × 4
= 530.92
= 531 grains (approx.)
EXERCISE 11.1
Question 1: Diameter of the base of a cone is 10.5 cm and its slant height is 10 cm. Find its curved surface area.
Solution:
Radius r = 10.5/2 = 5.25 cm
Slant height l = 10 cm
Curved surface area = πrl
= (22/7) × 5.25 × 10
= (22/7) × 52.5
= 165 cm²
Question 2: Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is 24 m.
Solution:
Radius r = 24/2 = 12 m
Slant height l = 21 m
Total surface area = πr(l + r)
= (22/7) × 12 × (21 + 12)
= (22/7) × 12 × 33
= (22/7) × 396
= 1244.57 m² (approx.)
Question 3: Curved surface area of a cone is 308 cm² and its slant height is 14 cm. Find (i) radius of the base and (ii) total surface area of the cone.
Solution:
(i) Curved surface area = πrl
308 = (22/7) × r × 14
308 = 44r
r = 308/44
r = 7 cm
(ii) Base area = πr²
= (22/7) × 7²
= (22/7) × 49
= 154 cm²
Total surface area = Curved surface area + Base area
= 308 + 154
= 462 cm²
Question 4: A conical tent is 10 m high and the radius of its base is 24 m. Find (i) slant height of the tent, (ii) cost of the canvas required to make the tent, if the cost of 1 m² canvas is ₹70.
Solution:
(i) h = 10 m, r = 24 m
l = √(h² + r²)
l = √(10² + 24²)
l = √(100 + 576)
l = √676
l = 26 m
(ii) Canvas required = Curved surface area = πrl
= (22/7) × 24 × 26
= (22/7) × 624
= 1961.14 m² (approx.)
Cost = 1961.14 × 70
= ₹137,280 (approx.)
Question 5: What length of tarpaulin 3 m wide will be required to make conical tent of height 8 m and base radius 6 m? Assume extra length for stitching margins and wastage is approximately 20 cm. (Use π = 3.14)
Solution:
h = 8 m, r = 6 m
Slant height l = √(h² + r²)
l = √(8² + 6²)
l = √(64 + 36)
l = √100
l = 10 m
Curved surface area = πrl
= 3.14 × 6 × 10
= 188.4 m²
Length required = Area/Width
= 188.4/3
= 62.8 m
Adding wastage = 62.8 + 0.2
= 63 m
Question 6: The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find the cost of white-washing its curved surface at the rate of ₹210 per 100 m².
Solution:
l = 25 m
Diameter = 14 m, so r = 7 m
Curved surface area = πrl
= (22/7) × 7 × 25
= 550 m²
Cost = (550/100) × 210
= 5.5 × 210
= ₹1,155
Question 7: A joker’s cap is in the form of a right circular cone of base radius 7 cm and height 24 cm. Find the area of the sheet required to make 10 such caps.
Solution:
r = 7 cm, h = 24 cm
Slant height l = √(h² + r²)
l = √(24² + 7²)
l = √(576 + 49)
l = √625
l = 25 cm
Area for one cap = πrl
= (22/7) × 7 × 25
= 550 cm²
Area for 10 caps = 550 × 10
= 5,500 cm²
Question 8: A bus stop is barricaded using 50 hollow cones made of recycled cardboard. Each cone has base diameter 40 cm and height 1 m. If the outer side is to be painted at ₹12 per m², find the cost. (Use π = 3.14 and √1.04 = 1.02)
Solution:
Diameter = 40 cm = 0.4 m
Radius r = 0.2 m
Height h = 1 m
Slant height l = √(h² + r²)
l = √(1² + 0.2²)
l = √(1 + 0.04)
l = √1.04
l = 1.02 m
Curved surface area of one cone = πrl
= 3.14 × 0.2 × 1.02
= 0.64056 m²
Total area for 50 cones = 50 × 0.64056
= 32.028 m²
Cost = 32.028 × 12
= ₹384.336
= ₹384 (approx.)
11.2 Surface Area of a Sphere
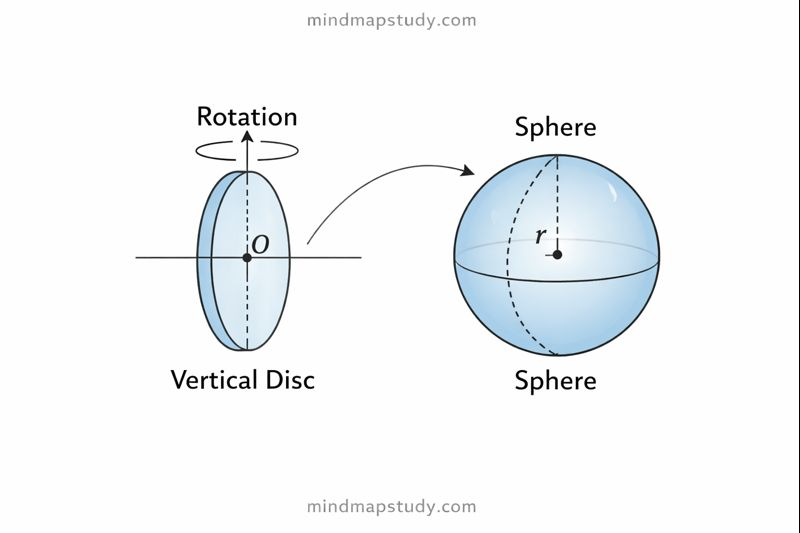
Understanding a Sphere
A circle is a plane figure where every point lies at constant distance (radius) from a fixed point (centre). When you rotate a circular disc about its diameter, you get a sphere.
A sphere is a three-dimensional figure made up of all points in space that lie at constant distance (radius r) from a fixed point (centre).
Deriving Surface Area Formula
Through an activity with a string wound around a ball, we discover that the string completely fills exactly four circles of the same radius as the ball.
This suggests:
Surface area of sphere = 4 × Area of circle
= 4 × πr²
Surface Area of a Sphere = 4πr²
where r is the radius of the sphere.
Understanding a Hemisphere
When you slice a solid sphere exactly through the middle, you get two equal halves called hemispheres.
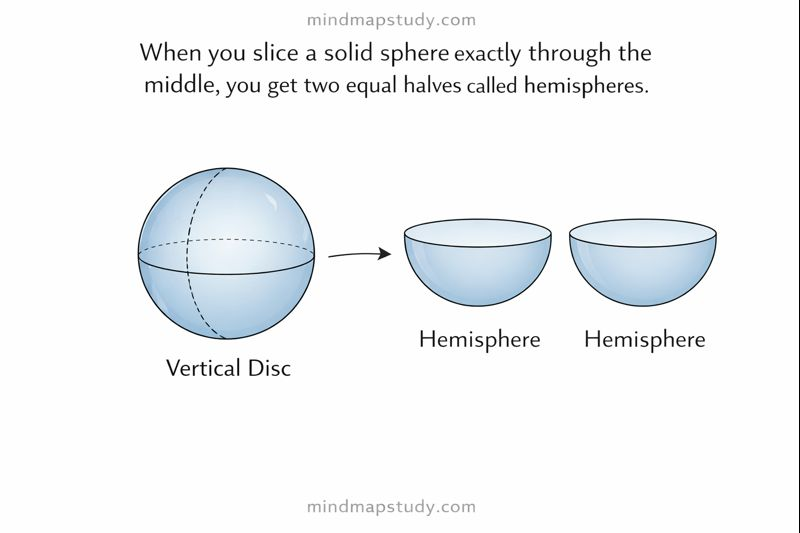
A hemisphere has two surfaces:
- Curved surface (half of sphere surface)
- Flat circular base
Curved Surface Area of Hemisphere = 2πr²
Total Surface Area of Hemisphere = 2πr² + πr² = 3πr²
Example 4
Find the surface area of a sphere of radius 7 cm.
Solution:
Surface area = 4πr²
= 4 × (22/7) × 7 × 7 cm²
= 4 × 22 × 7 cm²
= 616 cm²
Example 5
Find (i) the curved surface area and (ii) the total surface area of a hemisphere of radius 21 cm.
Solution:
(i) Curved surface area = 2πr²
= 2 × (22/7) × 21 × 21 cm²
= 2 × 22 × 3 × 21 cm²
= 2,772 cm²
(ii) Total surface area = 3πr²
= 3 × (22/7) × 21 × 21 cm²
= 3 × 22 × 3 × 21 cm²
= 4,158 cm²
Example 6
The hollow sphere in which a circus motorcyclist performs stunts has diameter 7 m. Find the area available for riding.
Solution:
Diameter = 7 m
Radius r = 3.5 m
Riding area = Surface area of sphere
= 4πr²
= 4 × (22/7) × 3.5 × 3.5 m²
= 4 × (22/7) × 12.25 m²
= 154 m²
Example 7
A hemispherical dome needs to be painted. If the circumference of the base is 17.6 m, find the cost of painting at ₹5 per 100 cm².
Solution:
Circumference = 2πr = 17.6 m
r = 17.6 × 7/(2 × 22)
r = 17.6 × 7/44
r = 2.8 m
Curved surface area = 2πr²
= 2 × (22/7) × 2.8 × 2.8 m²
= 2 × 22 × 0.4 × 2.8 m²
= 49.28 m²
Cost of painting 1 m² = ₹500 (since 100 cm² costs ₹5)
Total cost = 49.28 × 500
= ₹24,640
EXERCISE 11.2
Question 1: Find the surface area of a sphere of radius: (i) 10.5 cm (ii) 5.6 cm (iii) 14 cm
Solution:
Surface area = 4πr²
(i) = 4 × (22/7) × 10.5 × 10.5
= 4 × (22/7) × 110.25
= 1,386 cm²
(ii) = 4 × (22/7) × 5.6 × 5.6
= 4 × (22/7) × 31.36
= 394.24 cm²
(iii) = 4 × (22/7) × 14 × 14
= 4 × 22 × 2 × 14
= 2,464 cm²
Question 2: Find the surface area of a sphere of diameter: (i) 14 cm (ii) 21 cm (iii) 3.5 m
Solution:
(i) Radius = 7 cm
Surface area = 4 × (22/7) × 7 × 7
= 616 cm²
(ii) Radius = 10.5 cm
Surface area = 4 × (22/7) × 10.5 × 10.5
= 1,386 cm²
(iii) Radius = 1.75 m
Surface area = 4 × (22/7) × 1.75 × 1.75
= 38.5 m²
Question 3: Find the total surface area of a hemisphere of radius 10 cm. (Use π = 3.14)
Solution:
Total surface area = 3πr²
= 3 × 3.14 × 10 × 10
= 3 × 3.14 × 100
= 942 cm²
Question 4: The radius of a spherical balloon increases from 7 cm to 14 cm as air is pumped into it. Find the ratio of surface areas in the two cases.
Solution:
Initial surface area = 4π(7)²
= 196π cm²
Final surface area = 4π(14)²
= 784π cm²
Ratio = 196π : 784π
= 1 : 4
Question 5: A hemispherical bowl made of brass has inner diameter 10.5 cm. Find the cost of tin-plating it on the inside at ₹16 per 100 cm².
Solution:
Diameter = 10.5 cm
Radius r = 5.25 cm
Curved surface area = 2πr²
= 2 × (22/7) × 5.25 × 5.25
= 2 × (22/7) × 27.5625
= 173.25 cm²
Cost = (173.25/100) × 16
= 1.7325 × 16
= ₹27.72
Question 6: Find the radius of a sphere whose surface area is 154 cm².
Solution:
4πr² = 154
4 × (22/7) × r² = 154
(88/7) × r² = 154
r² = 154 × 7/88
r² = 1078/88
r² = 12.25
r = 3.5 cm
Question 7: The diameter of the moon is approximately one-fourth of the diameter of the earth. Find the ratio of their surface areas.
Solution:
Let earth’s diameter = 4d, then moon’s diameter = d
Earth’s radius = 2r, moon’s radius = r
Earth’s surface area = 4π(2r)² = 16πr²
Moon’s surface area = 4π(r)² = 4πr²
Ratio = 16πr² : 4πr²
= 4 : 1
Question 8: A hemispherical bowl is made of steel, 0.25 cm thick. The inner radius is 5 cm. Find the outer curved surface area.
Solution:
Inner radius = 5 cm
Outer radius = 5 + 0.25 = 5.25 cm
Outer curved surface area = 2πr²
= 2 × (22/7) × 5.25 × 5.25
= 2 × (22/7) × 27.5625
= 173.25 cm²
Question 9: A right circular cylinder just encloses a sphere of radius r. Find (i) surface area of the sphere, (ii) curved surface area of the cylinder, (iii) ratio of the areas.
Solution:
When cylinder encloses sphere:
Cylinder radius = r
Cylinder height = 2r
(i) Surface area of sphere = 4πr²
(ii) Curved surface area of cylinder = 2πrh
= 2πr(2r)
= 4πr²
(iii) Ratio = 4πr² : 4πr²
= 1 : 1
11.3 Volume of a Right Circular Cone
Understanding Cone Volume
Through an experiment with a hollow cone and cylinder of same base radius and height, we discover that filling the cone with sand three times exactly fills the cylinder.
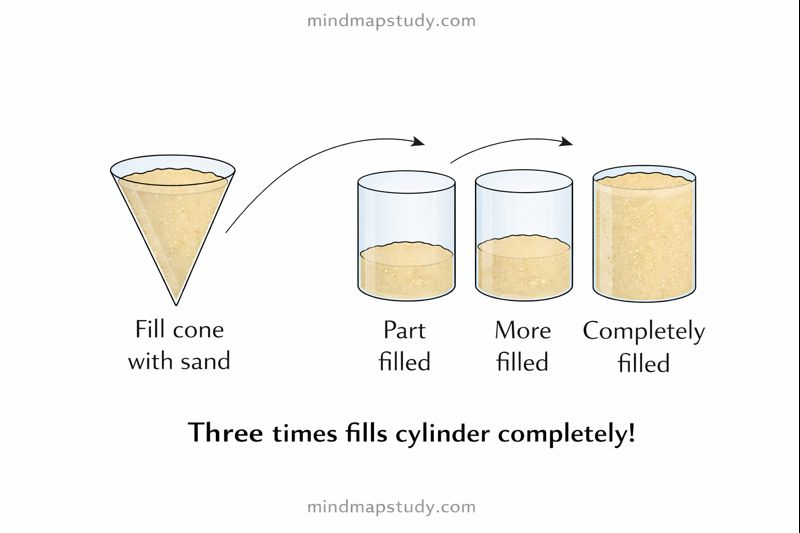
This shows: Volume of cone = (1/3) × Volume of cylinder
Volume of a Cone = (1/3)πr²h
where r is base radius and h is height.
Example 8
The height and slant height of a cone are 21 cm and 28 cm respectively. Find the volume.
Solution:
From l² = r² + h²:
r² = l² – h²
r² = 28² – 21²
r² = 784 – 441
r² = 343
r = √343 = 7√7 cm
Volume = (1/3)πr²h
= (1/3) × (22/7) × 343 × 21 cm³
= (1/3) × 22 × 49 × 21 cm³
= 7,546 cm³
Example 9
Monica has a piece of canvas of area 551 m². She makes a conical tent with base radius 7 m. Assuming 1 m² is lost in wastage, find the volume of the tent.
Solution:
Available canvas = 551 – 1 = 550 m²
Base radius r = 7 m
Tent has only curved surface:
πrl = 550
(22/7) × 7 × l = 550
22l = 550
l = 25 m
From l² = r² + h²:
h² = l² – r²
h² = 25² – 7²
h² = 625 – 49
h² = 576
h = 24 m
Volume = (1/3)πr²h
= (1/3) × (22/7) × 7 × 7 × 24 m³
= (1/3) × 22 × 7 × 24 m³
= 1,232 m³
EXERCISE 11.3
Question 1: Find the volume of the right circular cone with (i) radius 6 cm, height 7 cm (ii) radius 3.5 cm, height 12 cm
Solution:
Volume = (1/3)πr²h
(i) = (1/3) × (22/7) × 6 × 6 × 7
= (1/3) × 22 × 6 × 6
= 264 cm³
(ii) = (1/3) × (22/7) × 3.5 × 3.5 × 12
= (1/3) × (22/7) × 12.25 × 12
= 154 cm³
Question 2: Find the capacity in litres of a conical vessel with (i) radius 7 cm, slant height 25 cm (ii) height 12 cm, slant height 13 cm
Solution:
(i) Find h from l² = r² + h²:
h² = 25² – 7²
h² = 625 – 49 = 576
h = 24 cm
Volume = (1/3) × (22/7) × 7 × 7 × 24
= 1,232 cm³
= 1.232 litres
(ii) Find r from l² = r² + h²:
r² = 13² – 12²
r² = 169 – 144 = 25
r = 5 cm
Volume = (1/3) × (22/7) × 5 × 5 × 12
= 314.29 cm³ (approx.)
= 0.314 litres
Question 3: The height of a cone is 15 cm. If its volume is 1570 cm³, find the radius. (Use π = 3.14)
Solution:
(1/3) × π × r² × h = 1570
(1/3) × 3.14 × r² × 15 = 1570
15.7r² = 1570
r² = 100
r = 10 cm
Question 4: If the volume of a cone of height 9 cm is 48π cm³, find the diameter.
Solution:
(1/3) × π × r² × 9 = 48π
3πr² = 48π
r² = 16
r = 4 cm
Diameter = 8 cm
Question 5: A conical pit of top diameter 3.5 m is 12 m deep. What is its capacity in kilolitres?
Solution:
Radius r = 1.75 m
Height h = 12 m
Volume = (1/3) × (22/7) × 1.75 × 1.75 × 12
= (1/3) × (22/7) × 3.0625 × 12
= 38.5 m³
= 38,500 litres
= 38.5 kilolitres
Question 6: Volume of a cone is 9856 cm³. If diameter of base is 28 cm, find (i) height (ii) slant height (iii) curved surface area
Solution:
Radius r = 14 cm
(i) (1/3) × (22/7) × 14 × 14 × h = 9856
(1/3) × 22 × 2 × 14 × h = 9856
(616/3)h = 9856
h = 9856 × 3/616
h = 48 cm
(ii) l = √(r² + h²)
l = √(14² + 48²)
l = √(196 + 2304)
l = √2500
l = 50 cm
(iii) Curved surface area = πrl
= (22/7) × 14 × 50
= 2,200 cm²
Question 7: A right triangle ABC with sides 5 cm, 12 cm and 13 cm is revolved about the side 12 cm. Find the volume of the solid.
Solution:
When revolved about 12 cm side:
Height h = 12 cm
Radius r = 5 cm
Volume = (1/3) × (22/7) × 5 × 5 × 12
= (1/3) × (22/7) × 25 × 12
= (1/3) × (22/7) × 300
= 314.29 cm³ (approx.)
Question 8: If the triangle in Question 7 is revolved about the side 5 cm, find the volume. Find the ratio of volumes.
Solution:
When revolved about 5 cm side:
Height h = 5 cm
Radius r = 12 cm
Volume = (1/3) × (22/7) × 12 × 12 × 5
= (1/3) × (22/7) × 144 × 5
= 754.29 cm³ (approx.)
Ratio of volumes = 314.29 : 754.29
= 5 : 12
Question 9: A heap of wheat is conical with diameter 10.5 m and height 3 m. Find its volume. Find the canvas area required to cover it.
Solution:
Radius r = 5.25 m
Height h = 3 m
Volume = (1/3) × (22/7) × 5.25 × 5.25 × 3
= (1/3) × (22/7) × 27.5625 × 3
= 86.625 m³
For canvas, find slant height:
l = √(r² + h²)
l = √(5.25² + 3²)
l = √(27.5625 + 9)
l = √36.5625
l = 6.05 m (approx.)
Canvas area = πrl
= (22/7) × 5.25 × 6.05
= 99.825 m² (approx.)
11.4 Volume of a Sphere
Understanding Sphere Volume
Through water displacement experiment, we discover that when a sphere is immersed in water, the volume of water displaced equals (4/3)πr³.
Volume of a Sphere = (4/3)πr³
where r is the radius.
Since hemisphere is half of sphere:
Volume of a Hemisphere = (2/3)πr³
Example 10
Find the volume of a sphere of radius 11.2 cm.
Solution:
Volume = (4/3)πr³
= (4/3) × (22/7) × 11.2 × 11.2 × 11.2 cm³
= (4/3) × (22/7) × 1404.928 cm³
= 5,887.32 cm³ (approx.)
Example 11
A shot-putt is a metallic sphere of radius 4.9 cm. If density of metal is 7.8 g per cm³, find the mass.
Solution:
Volume = (4/3)πr³
= (4/3) × (22/7) × 4.9 × 4.9 × 4.9 cm³
= 493 cm³ (approx.)
Mass = Volume × Density
= 493 × 7.8 g
= 3,845.44 g
= 3.85 kg (approx.)
Example 12
A hemispherical bowl has radius 3.5 cm. What volume of water would it contain?
Solution:
Volume = (2/3)πr³
= (2/3) × (22/7) × 3.5 × 3.5 × 3.5 cm³
= (2/3) × (22/7) × 42.875 cm³
= 89.8 cm³ (approx.)
EXERCISE 11.4
Question 1: Find the volume of a sphere whose radius is (i) 7 cm (ii) 0.63 m
Solution:
Volume = (4/3)πr³
(i) = (4/3) × (22/7) × 7 × 7 × 7
= (4/3) × 22 × 49
= 1,437.33 cm³ (approx.)
(ii) = (4/3) × (22/7) × 0.63 × 0.63 × 0.63
= 1.047 m³ (approx.)
Question 2: Find the amount of water displaced by a solid spherical ball of diameter (i) 28 cm (ii) 0.21 m
Solution:
(i) Radius = 14 cm
Volume = (4/3) × (22/7) × 14 × 14 × 14
= 11,498.67 cm³ (approx.)
(ii) Radius = 0.105 m
Volume = (4/3) × (22/7) × 0.105 × 0.105 × 0.105
= 0.004851 m³ (approx.)
Question 3: Diameter of a metallic ball is 4.2 cm. What is the mass if density is 8.9 g per cm³?
Solution:
Radius = 2.1 cm
Volume = (4/3) × (22/7) × 2.1 × 2.1 × 2.1
= 38.808 cm³
Mass = 38.808 × 8.9
= 345.39 g
Question 4: The diameter of moon is approximately one-fourth of earth’s diameter. What fraction of earth’s volume is moon’s volume?
Solution:
Let earth diameter = 4d, moon diameter = d
Earth radius = 2r, moon radius = r
Moon volume = (4/3)πr³
Earth volume = (4/3)π(2r)³ = (4/3)π × 8r³
Fraction = [(4/3)πr³] / [(4/3)π × 8r³]
= 1/64
Question 5: How many litres of milk can a hemispherical bowl of diameter 10.5 cm hold?
Solution:
Radius = 5.25 cm
Volume = (2/3) × (22/7) × 5.25 × 5.25 × 5.25
= 303.1875 cm³
= 0.303 litres (approx.)
Question 6: A hemispherical tank is made of iron sheet 1 cm thick. If inner radius is 1 m, find volume of iron used.
Solution:
Inner radius r = 1 m = 100 cm
Outer radius R = 101 cm
Volume of iron = (2/3)π(R³ – r³)
= (2/3) × (22/7) × (101³ – 100³)
= (2/3) × (22/7) × (1030301 – 1000000)
= (2/3) × (22/7) × 30301
= 63,617.14 cm³ (approx.)
Question 7: Find the volume of a sphere whose surface area is 154 cm².
Solution:
4πr² = 154
r² = 154 × 7/(4 × 22)
r² = 1078/88
r² = 12.25
r = 3.5 cm
Volume = (4/3) × (22/7) × 3.5 × 3.5 × 3.5
= 179.67 cm³ (approx.)
Question 8: A hemispherical dome was white-washed at cost ₹4,989.60. If cost is ₹20 per m², find (i) inside surface area (ii) volume of air inside.
Solution:
(i) Surface area = Cost / Rate
= 4989.60 / 20
= 249.48 m²
Curved surface area = 2πr²
249.48 = 2 × (22/7) × r²
r² = 249.48 × 7/(2 × 22)
r² = 39.69
r = 6.3 m
(ii) Volume = (2/3)πr³
= (2/3) × (22/7) × 6.3 × 6.3 × 6.3
= 523.908 m³ (approx.)
Question 9: Twenty-seven solid iron spheres, each of radius r and surface area S are melted to form a sphere with surface area S’. Find (i) radius r’ of new sphere (ii) ratio of S and S’.
Solution:
(i) Total volume = 27 × (4/3)πr³
= (4/3)π(r’)³
27 × (4/3)πr³ = (4/3)π(r’)³
27r³ = (r’)³
r’ = 3r
(ii) S = 4πr²
S’ = 4π(3r)² = 36πr²
Ratio S : S’ = 4πr² : 36πr²
= 1 : 9
Question 10: A capsule of medicine is spherical with diameter 3.5 mm. How much medicine (in mm³) is needed to fill it?
Solution:
Radius = 1.75 mm
Volume = (4/3) × (22/7) × 1.75 × 1.75 × 1.75
= 22.458 mm³ (approx.)
11.5 Summary
Formulas covered in this chapter:
- Curved surface area of a cone = πrl
- Total surface area of a right circular cone = πr(l + r)
- Surface area of a sphere = 4πr²
- Curved surface area of a hemisphere = 2πr²
- Total surface area of a hemisphere = 3πr²
- Volume of a cone = (1/3)πr²h
- Volume of a sphere = (4/3)πr³
- Volume of a hemisphere = (2/3)πr³
where l = slant height, r = radius, h = height
Download Free Mind Map from the link below
This mind map contains all important topics of this chapter
Visit our Class 9 Maths page for free mind maps of all Chapters
