What is Mathematical Modelling?
Mathematical modelling is the process of taking a real-world problem and converting it into a mathematical problem, solving it, and then interpreting the solution back into real-world terms.
Think of it as a bridge between your everyday life and the world of mathematics!
Simple Definition: A mathematical model is a mathematical relation (equation, formula, or graph) that describes a real-life situation.
Real-Life Applications of Mathematical Modelling:
- Launching satellites into space
- Predicting monsoon arrivals
- Controlling vehicle pollution
- Reducing traffic jams in big cities
- Banking and finance calculations
- Weather forecasting
- Medical treatment planning
- Civil engineering projects
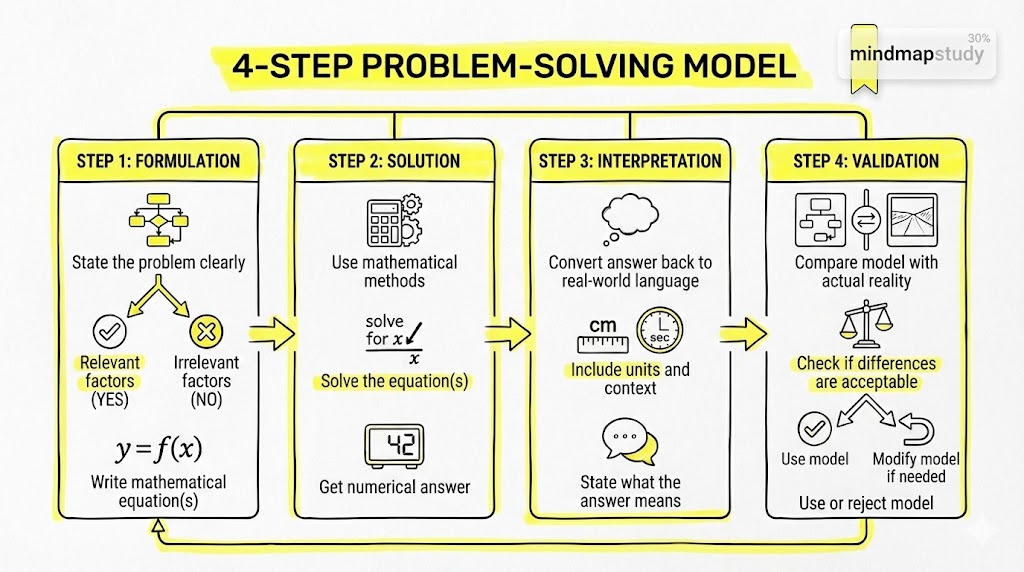
The Four Steps of Mathematical Modelling
Step 1: Formulation (Understanding the Problem)
In this step, you:
- State the Problem Clearly: Write down exactly what you need to find
- Identify Relevant Factors: Decide which quantities matter and which you can ignore
- Create Mathematical Description: Write the problem as one or more mathematical equations
Key Question: “What factors really matter for solving this problem?”
Example of Relevant vs Irrelevant Factors:
| Situation | Relevant Factors | Irrelevant Factors |
|---|---|---|
| Calculating petrol needed for a journey | Distance to travel, fuel consumption rate | Car color, driver’s name, music playing |
| Finding simple interest earned | Principal amount, Rate of interest, Time period | Bank building, teller’s age |
| Boat speed in a river | Upstream/downstream speeds, river speed | Boat color, number of passengers |
Step 2: Solution (Solving the Mathematical Problem)
In this step, you:
- Use Mathematical Knowledge: Apply algebra, geometry, or other math concepts
- Solve the Equations: Find the value(s) that satisfy your mathematical equations
- Get Numerical Answer: Obtain the mathematical solution
Step 3: Interpretation (Understanding the Result)
In this step, you:
- Convert Back to Real-World Language: Explain what your mathematical answer means in the original problem
- Check if Answer Makes Sense: Does the answer logically fit the real situation?
- State Your Conclusion: Give a clear, practical answer
Step 4: Validation (Checking Against Reality)
In this step, you:
- Compare with Reality: Check if your mathematical model matches what actually happens
- Test Your Model: If possible, verify with known data or observations
- Modify if Needed: If the model doesn’t match reality well, go back to Step 1 and improve your equations
- Accept or Reject: Decide if the model is good enough to use
This step is the most important difference between solving regular word problems and mathematical modelling!
Real-World Examples (Solved Step-by-Step)
Example 1: Direct Variation – Petrol Consumption
Problem: I travelled 432 km on 48 litres of petrol. How much petrol do I need for a 180 km journey?
Step 1: Formulation
- Problem: Find petrol needed for 180 km
- Relevant Factors: Distance travelled, petrol consumed
- Irrelevant Factors: Weather, road conditions (assumed constant)
- Mathematical Description:
- Let x = distance (in km)
- Let y = petrol needed (in litres)
- Direct variation: y = kx (where k is constant)
- From data: 48 = k × 432
- So: k = 48/432 = 1/9
- Formula: y = (1/9)x
Step 2: Solution
- For x = 180 km:
- y = (1/9) × 180
- y = 20 litres
Step 3: Interpretation
- Answer: 20 litres of petrol are needed for a 180 km journey
Step 4: Validation
- Assumption: The consumption rate remains the same
- If the 180 km route is different (mountains vs plains), the model might not work
- Model is valid only if conditions are similar to the original journey
Example 2: Simple Interest – Investment Problem
Problem: Sudhir invests ₹15,000 at 8% annual interest. He wants to buy a washing machine for ₹19,000. For how many years should he invest?
Step 1: Formulation
- Problem: Find the investment period needed
- Relevant Factors: Principal (₹15,000), Target amount (₹19,000), Interest rate (8%)
- Irrelevant Factors: Bank location, account number
- Mathematical Description:
- Simple Interest Formula: I = (P × n × r) / 100
- Where: P = ₹15,000, r = 8%, I = ₹19,000 – ₹15,000 = ₹4,000
- Formula: 4,000 = (15,000 × n × 8) / 100
- Simplifying: 4,000 = 1,200n
Step 2: Solution
- 1,200n = 4,000
- n = 4,000 / 1,200
- n = 3⅓ years (or 3 years 4 months)
Step 3: Interpretation
- Answer: Sudhir should invest for 3 years and 4 months to buy the washing machine
Step 4: Validation
- Assumption: Interest rate remains constant throughout
- Assumption: Machine price doesn’t increase
- Model works if these conditions hold true
Example 3: Upstream-Downstream – Boat Speed Problem
Problem: A motorboat takes 6 hours upstream and 5 hours downstream to cover the same distance. River speed is 2 km/h. Find the boat’s speed in still water.
Step 1: Formulation
- Problem: Find boat’s speed in still water
- Relevant Factors: Upstream time (6 h), Downstream time (5 h), River speed (2 km/h)
- Irrelevant Factors: Boat length, number of passengers, water temperature
- Mathematical Description:
- Let x = boat’s speed in still water (km/h)
- Let d = distance between towns (km)
- Upstream speed = (x – 2) km/h
- Downstream speed = (x + 2) km/h
- Distance = Speed × Time
- Equations:
- d = 6(x – 2) … Upstream
- d = 5(x + 2) … Downstream
Step 2: Solution
- Since both distances are equal:
- 6(x – 2) = 5(x + 2)
- 6x – 12 = 5x + 10
- 6x – 5x = 10 + 12
- x = 22 km/h
Step 3: Interpretation
- Answer: The boat’s speed in still water is 22 km/h
Step 4: Validation
- Check: Upstream speed = 22 – 2 = 20 km/h; Distance = 20 × 6 = 120 km ✓
- Check: Downstream speed = 22 + 2 = 24 km/h; Distance = 24 × 5 = 120 km ✓
- Model is valid!
Important Formulas and Concepts
Direct Variation Formula
y = kx (where k is a constant)
- “y varies directly with x”
- When x increases, y increases proportionally
Simple Interest Formula
I = (P × n × r) / 100
- I = Interest earned
- P = Principal (amount invested)
- n = Number of years
- r = Rate of interest per annum (%)
Distance-Speed-Time Formula
Distance = Speed × Time or d = st
Upstream-Downstream Relations
- Upstream speed = (boat speed – river speed)
- Downstream speed = (boat speed + river speed)
Identifying Relevant vs Irrelevant Factors
Strategy to Identify:
Relevant Factors Ask Yourself:
- Does this factor directly affect the answer?
- If I change this, will the answer change?
- Is this mentioned in the problem or necessary for calculation?
Irrelevant Factors:
- Would the answer be the same if I ignore this?
- Is this just additional descriptive information?
- Can solving the problem proceed without knowing this?
Quick Examples:
| Problem | Relevant Factors | Why Irrelevant Factors Don’t Matter |
|---|---|---|
| Calculating room floor area | Length and width of room, tile size | Wall color, furniture inside room |
| Finding travel time between cities | Distance between cities, average speed | Car model, driver’s age, music |
| Calculating monthly electricity bill | Units consumed, rate per unit | Meter brand, technician’s name |
Important Points
Point 1: Mathematical Models in Daily Life
Every formula you’ve learned in previous classes is a mathematical model:
- Simple Interest: I = Pnr/100
- Area of rectangle: A = length × width
- Perimeter formulas
- Distance formulas
Point 2: The Validation Step is Crucial
This step separates mathematical modelling from regular word problem solving. You must check if your mathematical answer makes sense in the real world.
Point 3: Assumptions Are Important
Every mathematical model requires assumptions. You must state these clearly:
- “We assume the speed remains constant”
- “We assume no external factors change”
- “We assume the given data is accurate”
Point 4: Models Can Be Improved
Your first model might not perfectly match reality. You can:
- Go back to Step 1 (Formulation)
- Identify what went wrong
- Modify your mathematical equations
- Test again in Step 4 (Validation)
Point 5: Balancing Accuracy and Usability
A good model:
- ✓ Is simple enough to use
- ✓ Is accurate enough for the purpose
- ✓ Doesn’t include unnecessary complexity
- ✓ Works within specified limitations
Advantages of Mathematical Modelling
- Cost-Effective: No need for expensive experiments
- Example: Testing pollution effects on Taj Mahal using models instead of real experiments
- Time-Saving: Get answers without waiting for real events
- Example: Predicting school infrastructure needs 5 years from now
- Safety: Avoid dangerous real-world testing
- Example: Testing earthquake resistance of buildings mathematically
- Predictions: Estimate future outcomes
- Example: Weather forecasting, population growth projections
- Understanding: Gain insights into how systems work
- Example: Understanding disease spread, traffic flow
- Decision Making: Help make better choices
- Example: Government policy planning, business strategy
Limitations of Mathematical Modelling
- Oversimplification: Real world is too complex to model perfectly
- A model is like a map – it shows some features but not all
- Assumption Errors: If assumptions are wrong, results are wrong
- Example: Assuming constant speed when speed actually varies
- Limited Tools: Some real situations are too complex to solve mathematically
- Example: Weather models are very complex, exact solutions are impossible
- Accuracy vs Simplicity Trade-off:
- Adding more details makes models more accurate but harder to use
- Adding fewer details makes models simpler but less accurate
- Limited Application Range: A model works only within certain limits
- A model for small distances might fail for very large distances
- A model for low speeds might fail at high speeds
- Data Limitations: Results depend on quality of input data
- Wrong or incomplete data leads to wrong conclusions
Quick Summary Table
| Aspect | Details |
|---|---|
| Definition | Converting real-world problems into mathematical problems |
| Number of Steps | 4 (Formulation, Solution, Interpretation, Validation) |
| When Useful | When real experiments are expensive, dangerous, or time-consuming |
| Key Formula | Different for each problem (direct variation, interest, distance, etc.) |
| Most Important Step | Validation (checking if model matches reality) |
| Common Assumption | That conditions remain constant or that neglected factors have minimal effect |
| Best Practice | Always check your answer against the real situation |
Tips for Success in Mathematical Modelling
1. Read the Problem Carefully
- Underline what you need to find
- Circle all given information
- Ask: “What exactly is being asked?”
2. Identify Relevant Information
- Ask: “Does this fact affect my answer?”
- Make a list of relevant factors
- Make a list of irrelevant factors
3. Write Mathematical Equations
- Use variables (x, y, etc.) clearly
- Show the relationship between variables
- Check: “Are my equations correct?”
4. Solve Step-by-Step
- Write all steps clearly
- Check calculations twice
- Use correct mathematical operations
5. Interpret Your Answer
- Convert back to real-world language
- Use appropriate units
- State complete answer: “The answer is _ because _“
6. Validate Before Concluding
- Check if answer is reasonable
- Test with given data if possible
- Ask: “Does this answer make sense?”
7. State Assumptions Clearly
- List all assumptions you made
- Explain why you made them
- Note limitations of your model
Important Questions & Answers
Q1: Why is the validation step important?
Answer: The validation step ensures your mathematical model actually represents the real situation accurately. Without it, you might get an answer that is mathematically correct but wrong in reality.
Q2: Can a mathematical model be perfect?
Answer: No, a mathematical model is always a simplification of reality. It can never perfectly represent the real world because real situations are too complex. But a good model is accurate enough for its intended purpose.
Q3: What should I do if my model doesn’t match reality?
Answer: Go back to Step 1 (Formulation) and:
- Check your assumptions
- Identify what factors you neglected
- Modify your mathematical equations
- Test again using validation
Q4: Is every formula in my textbook a mathematical model?
Answer: Yes! Every formula represents a mathematical relationship that describes a real-world situation. For example, the simple interest formula I = Pnr/100 is a mathematical model for how bank interest works.
Q5: Can I ignore some factors in the problem?
Answer: Yes, but only if they are truly irrelevant to the answer. A factor is irrelevant if:
- It doesn’t affect the final answer
- Its effect is so small that it can be neglected
- The problem would become impossible to solve if you included it
Q6: Why do scientists use mathematical models?
Answer: Scientists use mathematical models because:
- Real experiments are often expensive or impossible
- Mathematical models save time and money
- They help predict future events
- They allow testing dangerous scenarios safely
Q7: What’s the difference between a word problem and mathematical modelling?
Answer:
| Word Problem | Mathematical Modelling |
|---|---|
| Has all information ready to use | Must identify relevant information |
| Has 3 steps | Has 4 steps (includes validation) |
| Answer is usually final | Answer must be checked against reality |
| Usually simple and artificial | Usually complex and real-world |
Q8: How do I know if my assumptions are reasonable?
Answer: Your assumptions are reasonable if:
- They don’t change the problem significantly
- The real situation stays relatively constant
- The effect of ignored factors is very small
- Similar successful models use the same assumptions
Q9: What if the model takes too long to solve?
Answer: If your model is too complicated:
- You can simplify it (but lose accuracy)
- You can use approximate methods
- You can use computers/calculators
- Remember: Balance accuracy with practicality
Q10: Can two different models give different answers?
Answer: Yes, and this is normal! Different models may:
- Make different assumptions
- Consider different relevant factors
- Use different mathematical approaches
- Both could be “correct” within their own limitations
Real-World Application: Gender Equality in Education
This is a real example from the NCERT textbook about predicting girl student enrollment in primary schools.
The Situation:
The UN’s goal is to achieve 50% enrollment of girls in schools by 2015. India collects data year by year.
The Mathematical Model:
Using 10 years of data, scientists created an equation to predict future enrollment:
Enrollment % = 41.9 + 0.22n
Where n = number of years after 1991
Prediction:
By solving 50 = 41.9 + 0.22n, they predicted enrollment would reach 50% in the year 2027.
Validation:
They checked their model against actual data and found small differences of 0.3-0.5%. This was acceptable, so they used this model for predictions.
How to Score Well in Mathematical Modelling
In Examinations:
- ✓ Clearly state relevant and irrelevant factors
- ✓ Write all mathematical equations properly
- ✓ Show all steps in solution
- ✓ Interpret answer in real-world terms
- ✓ If possible, validate your answer
- ✓ State all assumptions you made
Common Mistakes to Avoid:
- ✗ Not identifying relevant factors
- ✗ Missing the validation step
- ✗ Not stating assumptions
- ✗ Wrong mathematical equations
- ✗ Calculation errors
- ✗ Not converting answer back to real-world terms
Practice Strategy:
- Solve 3-4 examples completely (all 4 steps)
- Identify patterns in similar problems
- Create your own real-world problems
- Exchange with classmates and solve theirs
- Explain your solution to someone else
Connection with Other Chapters
Mathematical modelling uses concepts from:
- Linear Equations: Writing and solving mathematical relationships
- Algebra: Using variables and formulas
- Geometry: Calculating areas, volumes, distances
- Trigonometry: Finding heights, angles in real situations
- Statistics: Using data to create models
Practice Problems
Exercise A2.1
Problem 1: A company can hire a computer for ₹2,000/month or buy for ₹25,000. After how many months is buying cheaper?
Solution Outline:
- Relevant: Monthly cost, purchase price
- Irrelevant: Computer brand, color
- Equation: 2,000n = 25,000
- Answer: n = 12.5 months (buy after 13 months)
Problem 2: Two cars travel toward each other at 40 km/h and 30 km/h. Distance between them is 100 km. When will they meet?
Solution Outline:
- Relevant: Speed of each car, distance between them
- Irrelevant: Car models, driver names
- Equation: 40t + 30t = 100
- Answer: t = 10/7 ≈ 1.43 hours
Problem 3: Moon is 384,000 km from Earth and orbits in 24 hours. Find orbital speed.
Solution Outline:
- Distance = 2πr = 2 × 3.14 × 384,000
- Distance = 2,411,520 km
- Speed = Distance / Time = 2,411,520 / 24 ≈ 100,480 km/h
Problem 4: Water heater uses ₹8/hour. Base electricity bill ₹1,000 (without heater), ₹1,240 (with heater). Average hours per day?
Solution Outline:
- Extra bill with heater = ₹1,240 – ₹1,000 = ₹240
- Hours of use per month = 240 / 8 = 30 hours
- Hours per day = 30 / 30 ≈ 1 hour
Download Free Mind Map from the link below
This mind map contains all important topics of this chapter
Visit our Class 9 Maths page for free mind maps of all Chapters
